이번에 논문을 정리한 것은 Spectral Normalization에 관한 논문입니다. 해당 논문은 수학적 지식, 특히 선형대수 파트가 많이 사용된 것 같고, 선형대수쪽에 아무래도 매번.. (학부수업때도 잘 못 습득함) 어려움을 겪다 보니 기본적인 rank나, Singular value가 어떤 의미를 갖는지 이해하는데 어려웠던 것 같네요. 논문을 읽고 나서도 확실하게 두 개념에 대해서는 정리가 되는 느낌은 아닙니다. 아무래도 선형대수를 한번 더.. 꼼꼼하게 봐야할 것 같고, 최대한 이해한대로 정리해서 업로드하니 틀린정보가 있을 수도 있다는 점 혹시나 검색을 통하여 읽고 계시다면 양해 부탁드립니다.
그리고 수식이 많이 깨지네요. 노션으로 할땐 괜찮았는데 ..
SNGAN
Spectral Normalization for Generative Adversarial Network
Abstract
- GAN의 문제점은 학습할때 불안정성이 발생한다는 것임
- 해당 논문에서는 Weight Normalization, 즉 Spectral normalization을 통해 Discriminaotr의 학습과정을 안정하게 하려 하였음
- 이러한 Normalization은 Computationally light , easy
- 기존 학습 안정화 테크닉보다 좋은 결과를 나타냄
Introduction
- GAN의 등장과 발전은 많은 부분의 task와 dataset에 적용되었음. 간단히 말해서, GAN은 주어진 target distribution을 흉내내는 distribution을 생성하는 모델의 프레임워크로써, generator와 discriminator를 가지고 있음
- 지속되어져 오고 있는 GAN의 학습 부분에서의 문제점은 Discriminator의 performance control에서 발생함
- 고차원 공간에서는, Discriminator가 생성한 density ratio estimation은 학습하는 동안 자주 부정확하고 불안정하며, Generator는 Multi-modal 구조의 target distribution을 학습하는 것에도 실패함
- 추가로, model distribution과 target distribution의 범위가 분리된 경우라면, Discriminator는 완벽하게 생성샘플과 데이터샘플을 구별할 수 있게됨
- 이러한 문제점들로 인해 저자들은 Discriminator 선택에 대한 여러가지 제한방식을 소개하게 되었다고 함
- 해당 논문에서는 새로운 Weight Normalization인 Spectral normalziation을 제안하였으며, 이는 Discriminator의 학습시 안정화를 도와줌
- Spectral Normalization에서 사용되는 Lipschitz constant는 해당 기법에서 사용되는 단 하나의 하이퍼 파라미터이며, 알고리즘은 강한 튜닝을 필요로 하지 않음
- 구현은 간단하고, 추가적인 Computational cost가 작음
- 해당 상수인 Lipschitz constant의 튜닝이 없어도 normalization은 잘 동작하였음
- 추가로 기술한 내용은 Spectral normalization가 비교해서 다른 regularization 방법들(Weight normalization, Weight clipping, Gradient penalty)이며, Complimentary regularization기법(Batch Normalization, Weight decay, Feature matching)이 없을때, 이러한 Spectral Normalization 기법이 어떤 결과를 내는지 나타내었음
Method
- 처음엔 GAN에 대한 theoretical groundwork에 대해 설명되어 있음
- Discriminator는 다음과 같은 Neural Network로 구성되어 있는데, theta는 Learning parameter (Weight) Set , a함수는 non-linear Activation function임. bias는 생략하여 나타내었음
- 따라서 마지막 output은 다음과 같은데, A는 Activation function으로써, Divergence of distance measure를 나타냄
- 그래서 GAN은 Generator와 Discriminator구조를 사용해서 를 사용. 자세한건 Goodfellow et al, Generative Adversarial Network 참고
- 머신러닝 학회는 Discriminator가 선택한 function space가 치명적으로 GAN의 퍼포먼스에 영향을 미치는 점을 확인하였고, 관심을 가지고 있음.
- 몇몇의 연구는 Boundedness의 중요성에 대해 설명했고, 예를 들어 기존 GAN에선 Discriminator의 derivative를 설명할 수 있음
- Input sample x로 정의된 Regularization term을 추가한 Discriminator의 Lipschitz 상수를 추가하는 방법으로 성공한 사례가 있으며, 해당 논문은 이런 방법을 따라 Discriminator의 탐색에 집중하였음
- Discriminator는 K-Lipschitz continuous function를 사용하여 나타냄
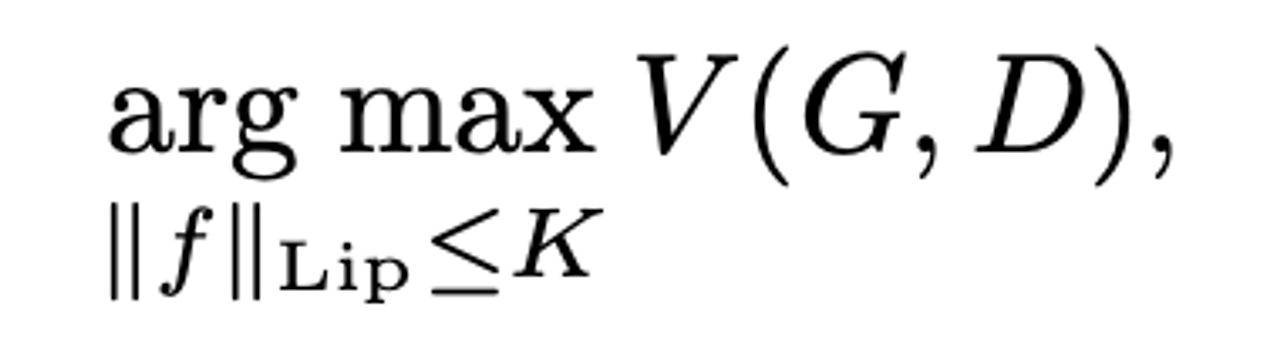
- Input based regularization은 비교적 쉬운 공식으로 이루어져 있지만, Generator의 생성범위나 Data distribution외의 영역에 대해 regularization을 적용할 수 없다는 제한이 있음
- 따라서 제안한 방법이 spectral normalization이며, 가중치를 normalizing 함으로써 해당 문제를 피할 수 있음
Spectral Normalization
- Spectral Normalization은 Discrimintator 함수의 Lipschitz 상수를 조절하는 것으로 진행하며, 이는 각 층에 spectral norm을 제한함으로써 조절할 수 있음
- 를 Lipschitz norm이라 하며,와 동일, 는 행렬 A의 spectral norm이라 정의함 Spectral norm 을 L2 Matrix norm이라 하였는데, 이는 A행렬의 가장 큰 특이값과 동일하다고 함
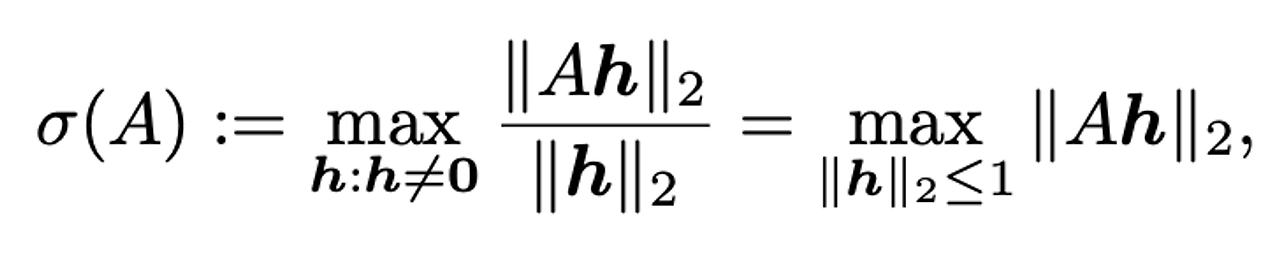
- ℎ, 즉 선형레이어 이며, 따라서 정리하면 으로 나타낼 수 있음
- Activation function인 은 1과 동일하며, 따라서 부등식 을 사용하여 최종적으로 Discriminator의 함수를 나타내면 아래와 같다.

- Discriminator 1⋅ℎ0→1ℎ0+2⋅ℎ1→2ℎ1+⋯
- Spectral normalization 은 가중치 행렬 W의 spectral norm을 normalize하는데, 이는 Lipschtiz constraint인 Lipschitz norm을 1로 하기 위해서임 Lipschitz constraint 가 위에서 설명한 이며, 가중치 행렬 W의 spectral norm, 즉 W행렬의 가장 큰 특이값과 동일하고, 이를 1로 하려고 하는 것임
- 정리하면, 은 가중치 행렬 W의 가장 큰 특이값으로 Normalize하려는 과정이며, 이는 가중치행렬 W를 가장 큰 특이값으로 나누어 최종 1로 bound하는 것임
- 이어서 Spectral normalization과 Spectral norm ‘Regularization’의 차이점을 강조했고, Regularization은 목적 함수에 명시적인 regularization을 더해주면서 spectral norm을 제한하는 반면, 해당 논문의 방법인 Spectral normalization은 normalized cost function의 derivative를 재구성하고, 목적함수를 재 작성함으로써 해당 방법이 cost function을 증강(augment)시키는 것을 확인할 수 있음
- 또한 Spectral Normalization에서 cost function은 sample data와 연관있는 regularization function인 반면, Spectral norm ‘Regularization’에선 regularization이 sample data와 연관이 없는(독립적)인 cost function을 사용함(이는 L2 Regularization, Lasso와 같음)
Fast approximation of the spectral norm
- Spectral norm은 가장 큰 특이값을 찾는 것이었으며, SVD를 통해서 이를 찾는 것은 매우 컴퓨터적인 요소가 큰 것을 확인하였음
- 따라서 대신에 power iteration이라는 방식을 사용하여 가장 큰 특이값을 찾도록 하였고, 해당 방식으로 작은 computational time으로 spectral norm을 추정할 수 있음을 확인하였음
Spectral Normalization VS Other regularization tech.
- 가중치 normalization은 각 가중치 벡터들의 행 벡터의 L2 norm을 normalize하는 방법임
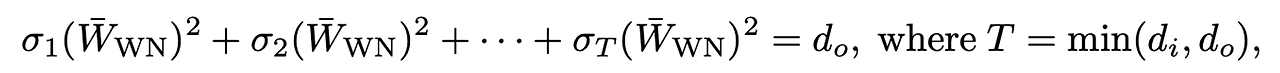
- 는 A행렬의 t번째 특이값임
- 이러한 normalization은 의도한 바 보다 꽤 큰 제한을 부과하는 단점이 있음.
- 만약 input, output shape를 가지고있는 weight normalize 행렬이라면, 이 최대일때 ∣2 값이 최대가 되는데, 이 말인 즉슨 여러 특이값(1,2, … T)까지 중 첫번째값만 value를 가지고 나머지 값들은 0 임을 나타냄
- 이와 같은 Weight normalization은 discriminator가 단 하나의 feature만 사용한다고 볼 수 있음
- input의 많은 norm을 유지하기 위해서 discriminator를 더 sensitive하게 만들어야하고, ℎ를 크게 만들어야하는데, Weight normalziation에선 이러한 것이 위와 같이 rank를 줄이는 결과를 냈고 적은 feature가 discriminator에 사용됨
- 따라서 Weight normalization과 많은 feature를 사용하는 것. 둘 사이의 견해차이가 존재하고, 몇몇 연구는 feature 감소를 무릅쓴 Weight normalization을 사용하는 반면, 해당 논문의 Spectral normalization은 이러한 논쟁에서 벗어나 생각하였음
- Lipschitz constant가 오직 가장 큰 특이값으로만 결정 되기 때문에 spectral norm은 rank과 독립적이고, parameter matrix가 많은 feature들을 갖게 해줌 또한 Spectral normalization이 더 많은 feature들을 선택할 수 있게 해주는데 이점이 있음
- Orthonormal regularization은 또 다른 regularization 방법인데, GAN의 학습과정을 안정화 시켜주며 아래의 수식을 adversarial 목적 함수에 더해주는 것으러 사용가능함

- 해당 regularization이 spectral normalization과 다른 점은 orthonormal regularization이 모든 특이값을 1로 하여 스펙트럼의 모든 정보를 없애버린다는 점에서 다름
- 반면 spectral normalization은 오직 스펙트럼을 축소하거나 늘림
- 또 다른 Regularization은 gradient penalty를 사용한 것이며 WGAN과 함께 사용하였음
- K-Lipschitz constant를 discriminator에 사용하여 목적함수를 local 1-Lipschitz constant를 갖도록 보상해주는 방향으로 사용
- local 1-Lipschitz constant를 갖는 부분은 discrete set of points: 으로, x’은 Generator distribution에서, x는 data distribution에서 온 값으로 서로 보간을 통해 정의함
- 이러한 접근은 generator의 distribution 범위에 강하게 종속된다는 단점이 있고, 당연히 generative distribution과 해당 생성 범위들은 점차적으로 학습에 의해서 바뀌지만, 이것이 이러한 regularization을 통해서 불안정해 질 수 있음
- 높은 learning rate들이 이러한 불안정성을 야기하였을 것으로 예상하였고, Spectral normalization이 operator space의 함수를 regularize함으로써 regularization의 효과를 더 안정적일 수 있도록 하였음
- Spectral normalization을 사용한 학습은 공격적인 학습률에도 쉽게 불안정해지지 않는 결과를 보여줬음
Experiments
- CIFAR-10과 STL-10을 사용해서 다른 normalization 방법과 비교해서 실험결과를 나타내었음
- Discriminator와 Generator에서는 convolutional neural network를 사용하였고, generator의 변수들은 batch normalization을 사용해서 학습시켰음
- 또한 다양한 목적함수를 사용해서 실험을 진행했음(Adversarial loss, hinge loss, WGAN-gradient penalty )

- IS와 FID값을 나타낸 것으로 각각 다른 모델, IS는 높을 수록 좋은결과를 나타내며, FID는 낮을 수록 좋은 결과를 나타냄. 결과를 확인해보면 Spectral normalization이 좋은 결과를 나타낸 것을 확인할 수 있음


- 다른 모델과 비교하여 나타낸 Spectral normalization의 효과

- 각 데이터셋을 사용해 보인 여러가지 방법 ( Weight clipping, Weight normalization, Spectral normalization)을 사용해서 특이값제곱에 얼마나 빨리 도달하는지 확인 가능: Spectral normalization이 가장 우세

- STL-10을 사용한 결과이며, feature map dimension의 변화에 따른 결과임
- 위 아래로 넓이가 표시 된 것은 결과의 표준편차를 나타낸 것이며, orthonormal regularization이 큰 feature map dimension에서 잘 동작하지 않는 이유가 해당 디자인이 모든 불필요한 차원까지 사용하도록 설계되었기 때문이라고 말하고 있음

- Learning curve를 나타낸 것이며, ImageNet 데이터를 사용해 SN-GAN과 Orthonormal을 사용한 일반 GAN에 대한 차이를 나타내는 곡선
Conclusion
- 해당 논문은 Spectral normalization을 GAN의 학습과정에서 안정시킬 수 있는 방법이라고 말하였음
- 해당 Normalization을 사용하면, 생성된 예시들은 더 다양하고, 더 나은 성능을 보여줌
- 해당 방법이 다른 방법들과 비교함에 더 조사를 진행하고, 해당 알고리즘을 더 크고 더 복잡한 데이터셋에 적용하는 것을 개선사항으로 생각하고 있음
주석 1. Density ratio estimation : Estimation of comparison with two densities that are in the same units
주석 2. Lipschitz continuous function: ∣ 을 만족하는 가장 작은 M이 Non-negative Lipschitz constant이며, 즉, 두 점 사이의 거리를 일정 비율, 일정 기울기 이상으로 올리지 않겠다는 뜻
주석 3. 특이값이 1이 된다는 것은? 원본 행렬의 크기를 1로 스케일링하겠다는 의미를 나타냄. 데이터의 크기를 정규화하는 효과를 나타내고, 크기를 일관되게 조정
주석 4. Generator 의 “Support” : 일반적으로 생성자가 생성할 수 있는 데이터 분포를 나타냄. 이미지특성, 생성된 이미지의 크기, 색상범위, 텍스쳐 등을 나타내고 따라서 다시말해, 생성자가 생성할 수 있는 데이터의 범위나 특성을 의미함!
주석 5. Power Iteration:
∴
if k goes to infinite,
확실히 학기중에 모든 것을 다하려니까 쉽지않네요. 다음번에 업로드할 논문은 DCGAN, 혹은 WGAN입니다.