오늘의 포스팅은 BigGAN에 대한 리뷰입니다. BigGAN은 GAN보다 큰 구조를 채택해서 더 좋은 결과를 나타내도록 하게 한 모델입니다.
논문에서 나온 방법들이 정확하게 하나하나 무엇인지 이해하는 것이 꽤 어려웠던 논문인거같습니다. 여러가지 짬뽕같은 느낌이라 그런지..
특히 선형대수의 Background가 탄탄해야 좋을 것 같다는 생각과 ,, 특히 특이값에 대한 이해가 있으면 좋을 것 같습니다.
최대한 제가 이해한 만큼 정리를 하였으니.. 만약 검색에 의해서 보시게 되신다면 틀린 정보가 있어도 다른 분들의 정보와 비교해서 보시면 좋을 것 같습니다.
BigGAN
Large Scale GAN Training for High Fidelity Natural Image Synthesis
Introduction
- GAN은 주어진 데이터로부터 학습된 모델을 사용하여 높은 재현율과 다양한 이미지를 생성하는 모델
- GAN의 학습은 Dynamic(생동적)하며, 거의 모든 Setup에 민감하게 영향을 받음 (Optimization para ~ model architecture)
- 해당 논문은 ImageNet data로 부터 생성된 이미지와 실제 이미지의 재현율과 다양성의 차이를 줄이고자 하였음
- 논문에서 구현한 모델은 상당한 Class-conditional GAN에서 상당한 향상을 이루어냈음
- IS, FID Score에서 모두 개선된 결과를 나타냄
- 더 큰 Dataset에서 학습을 진행하였고, 이 또한 잘 작동해 ImageNet에서 Transfer이 잘 된것도 확인할 수 있었음
Scaling Up GANs
- 해당 섹션에선 큰 모델과 큰 배치에서 얻을 수 있는 performance 개선을 얻기 위해 GAN의 학습 규모를 키우는 방법을 나타냄
- Baseline에서는 SA-GAN(Self attention GAN)을 사용
- Generator에 Class-condtional BatchNorm을 사용해 Class-information을 제공해주고, Discriminator에는 Projection을 사용해 Class-information을 제공해줌
- 최적화 설정은 learning rate를 이등분(halve)하여 수정하고, Generator의 한 스텝 대비 Discriminator의 두 스텝으로 진행되게끔 설정
- 평가는 Moving average를 이용해 0.9999의 가중치 감쇠를 사용, Generator의 가중치에 이를 반영
- 여기서 사용한 것은 이전 기법에 사용한 Xavier initialization 대신 Orthogonal Initialization을 사용
- 시작은 Baseline의 Batch size를 증가하는 것으로 시작했는데, 바로 benefit을 확인할 수 있었음
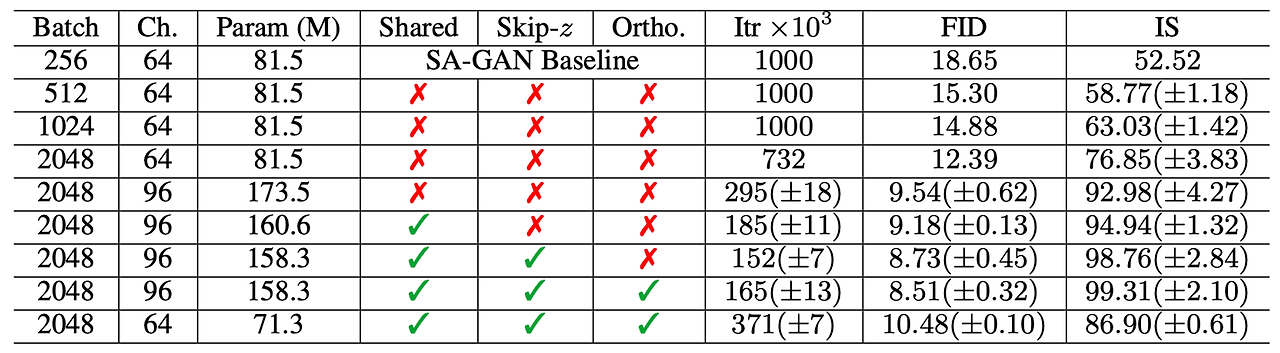
- 사진은 각 배치에 따른 결과인데, 1~4번째 행들은 배치가 증가함에 따라 성능이 증가함을 확인 가능
- 저자들은 추측하기를, 이러한 결과는 배치들이 더 많은 Mode를 커버하고, 더 나은 gradient를 제공한다는 것 때문이라고 함
- 하나의 부작용은 모델이 불안정해지고 학습이 붕괴되는 경우가 발생하였음
- 그 후 채널의 갯수를 늘려서 측정을 하였고 이 또한 성능이 증가하는 것을 확인할 수 있었음
- 저자들은 이것이 모델이 데이터의 복잡함과 관련되어 모델의 능력이 증가하여 그런 것으로 추측하였음
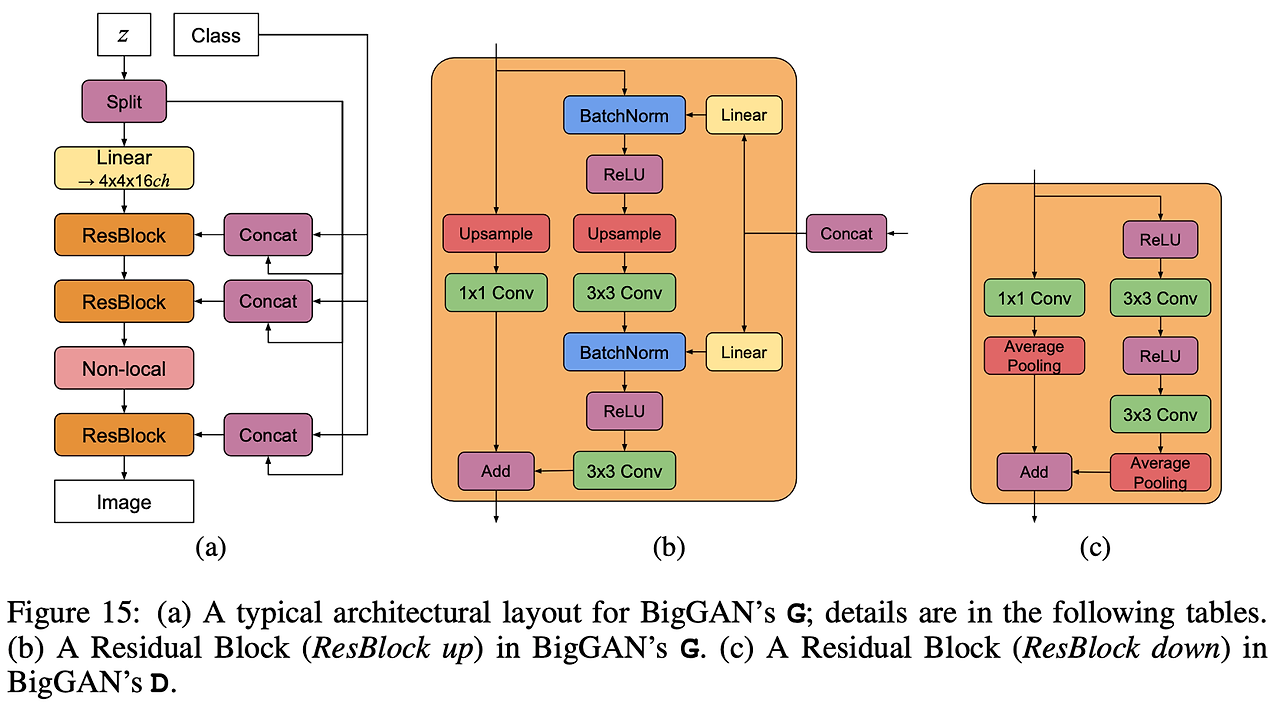
- 클래스 임베딩 C는 Generator의 Conditional BatchNorm layer에 포함되며, Generator는 많은 갯수의 가중치를 가지고 있음
- 해당 논문은 Shared embedding의 사용을 채택하였는데, 이는 각각 층의 gain과 bias들을 선형적으로 projected하는 것을 나타냄
- Shared embedding은 계산과 메모리의 비용을 줄여주는데, 학습의 속도 또한 향상시켜줌
- 그리고, Noise Vector Z에서 Generator 내 다수의 층으로 Direct Skip connection을 추가함
- 이러한 설계는 직관적으로 Generator가 latent space를 직접 사용할 수 있도록 하기 위함 이였고, 서로 다른 해상도와 서로 다른 레벨의 계층에서 오는 feature에 직접적으로 영향받기 위함이었음
- BigGAN에서 해당 설계는 Z를 쪼개어 해상도당 하나의 chunk로 나누어주고, 각각의 chunk들을 Conditional vector ‘C’로 결합시킴. 이러한 Vector는 BatchNorm의 Gain과 bias에 투영됨
- BigGAN-deep는 더 간단한 디자인을 사용하고, 모든 Noise Vector Z를 conditional Vector와 결합하며 BigGAN과 달리 chunk로의 쪼개는 과정이 없음
- Skip connection인 Skip-Z는 성능 향상을 나타내고, 학습 속도를 개선함
Detail: Trading off variety and fidelity with the truncation trick
- Latent를 사용하여 역전파를 사용하는 모델과 달리 GAN은 임의의 p(z)를 선택함.
- 가장 좋은 결과는 학습에 사용한 latent distribution과 다른 latent distribution을 샘플링을 위해 사용할 때 나왔음
- N(0,1)을 가지는 Z distribution으로 학습된 모델을 사용하고, Z를 truncated normal( 값 중 범위 밖의 버려진 값은 다시 범위에 들어가기 위해 resample)을 사용하여 sampling함
- 이러한 방식을 Truncation trick이라 하고, 이는 IS와 FID 성능을 개선시켰음
- Truncation trick은, 주어진 threshold를 설정하여 값을 resampling하고 (truncating Z vector) 이는 전체적인 샘플 퀄리티와 cost를 개선시킴

- 해당 그림은 그 결과를 증명: threshold가 감소하면, Z의 요소들은 ‘버림(Truncated toward Zero)’이 되고 각각의 샘플들은 Generator의 output 분포의 mode(가장 높은 빈도를 가진 값)에 접근하는 것을 증명
- Truncation trick은 세밀하고, Sample quality와 Sample 다양성 사이 Trade-off 선택을 하게해줌. 결과 그림에서 확인할 수 있듯이, threshold값이 커지면 다양성이 많아지고, threshold값이 작아지면 퀄리티가 좋아짐
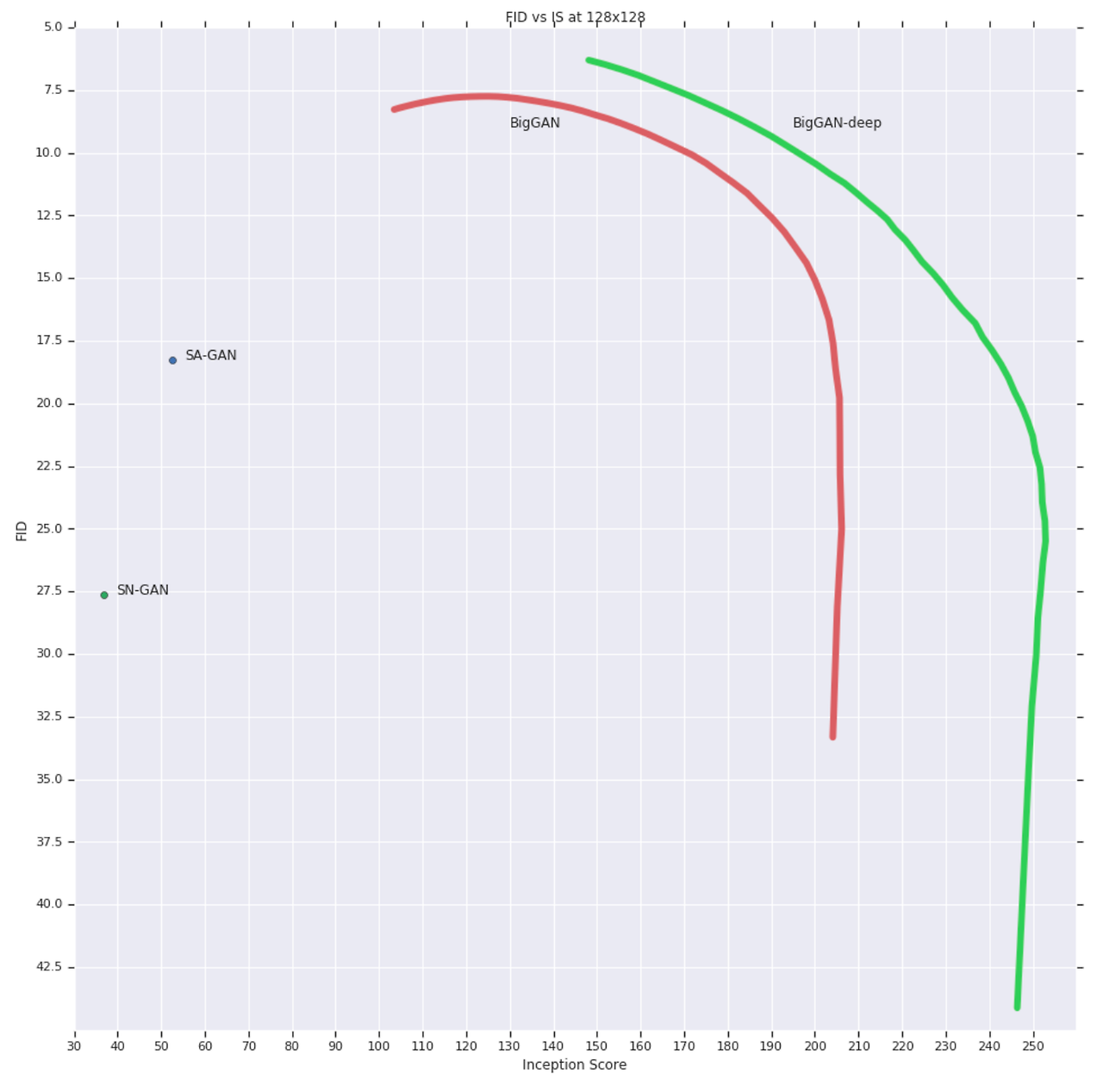
- IS는 다양성이 부족하다고 해서 영향받지않고 threshold를 줄이는 것은 IS의 증가로 이어지게 하였음. 또한 FID는 다양성에 영향을 받지만, 정확도에 대해 보상받기 때문에 FID의 성능에 대해서도 직관적으로 확인할 수 있었음. 추가로, ‘버림’의 사용과 다양성의 감소는 FID가 날카롭게 떨어지게하였음.
- 몇 몇 큰 모델은 truncation을 받아들이지 못하고 포화 구조를 만들어냄(Saturation artifacts). 이는 위의 그림 Figure 2 b에서 확인할 수 있고, 이것에 카운터를 날리기 위해 Generator를 조건화함으로써 Truncation을 강요함
- 이러한 조건화는 Z의 full space가 좋은 샘플로 output될 수 있도록 맵핑될 수 있도록 해주며, 해당 포화 구조를 해결해 줄 수 있는, 이러한 방법을 바로 Orthogonal Regularization( 직접 Orthogonality condition을 강요 )이라 함.
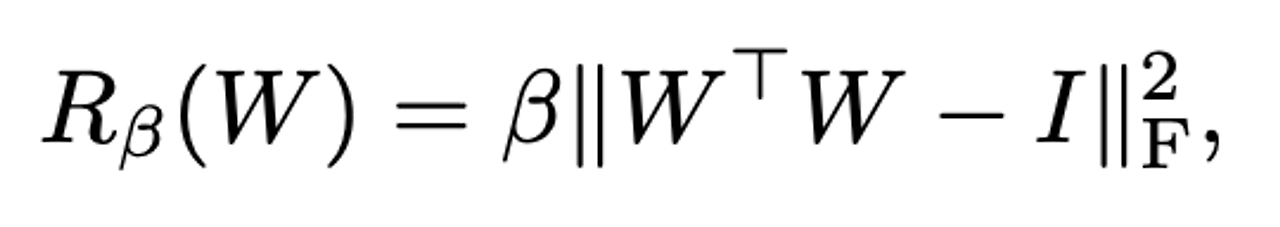
- W는 가중치 행렬이고 Beta는 하이퍼파리미터임. Orthogonal regularizaiton에서 약간의 변화를 주어 제한을 완화하기 위한 방법으로 사용
- 가장 효과가 좋았던 방법은 대각 성분을 제거함으로써, 필터 간 pairwise 코사인 유사도를 최소화 하는 것을 목표로 하였음(하지만 이는 norm에 대해선 제한을 주지않았음)
- 아래 수식이 해당 수식, 1은 모든 원소가 1인 행렬을 의미함(np.ones). Beta 또한 0.0001로 하였음.
- 이런 작은 penalty가 likelihood를 향상시켜 truncation을 진행할 수 있도록 하기에 충분함을 발견할 수 있었음
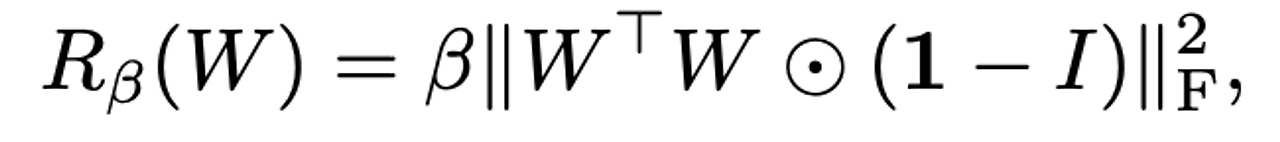
- 위에 첨부한, 표1에선 Ortho.가 있고없고에 따라 어떻게 성능차이가 나는지 확인할 수 있음(Orthogonal regularization이 없으면 16%의 경우만 truncation이 되게 하였고, 반대로 적용된 경우엔 60%)
Analysis
Characterizing Instability : The Generator
- 불안정성에 대한 원인을 체크하기 위해 가중치와 gradient, loss statistic을 모니터링 하였음
- 가장 유익한 정보를 얻기 위해 상위 3개의 특이값(Singular Value)를 각 가중치 행렬에서 찾았음
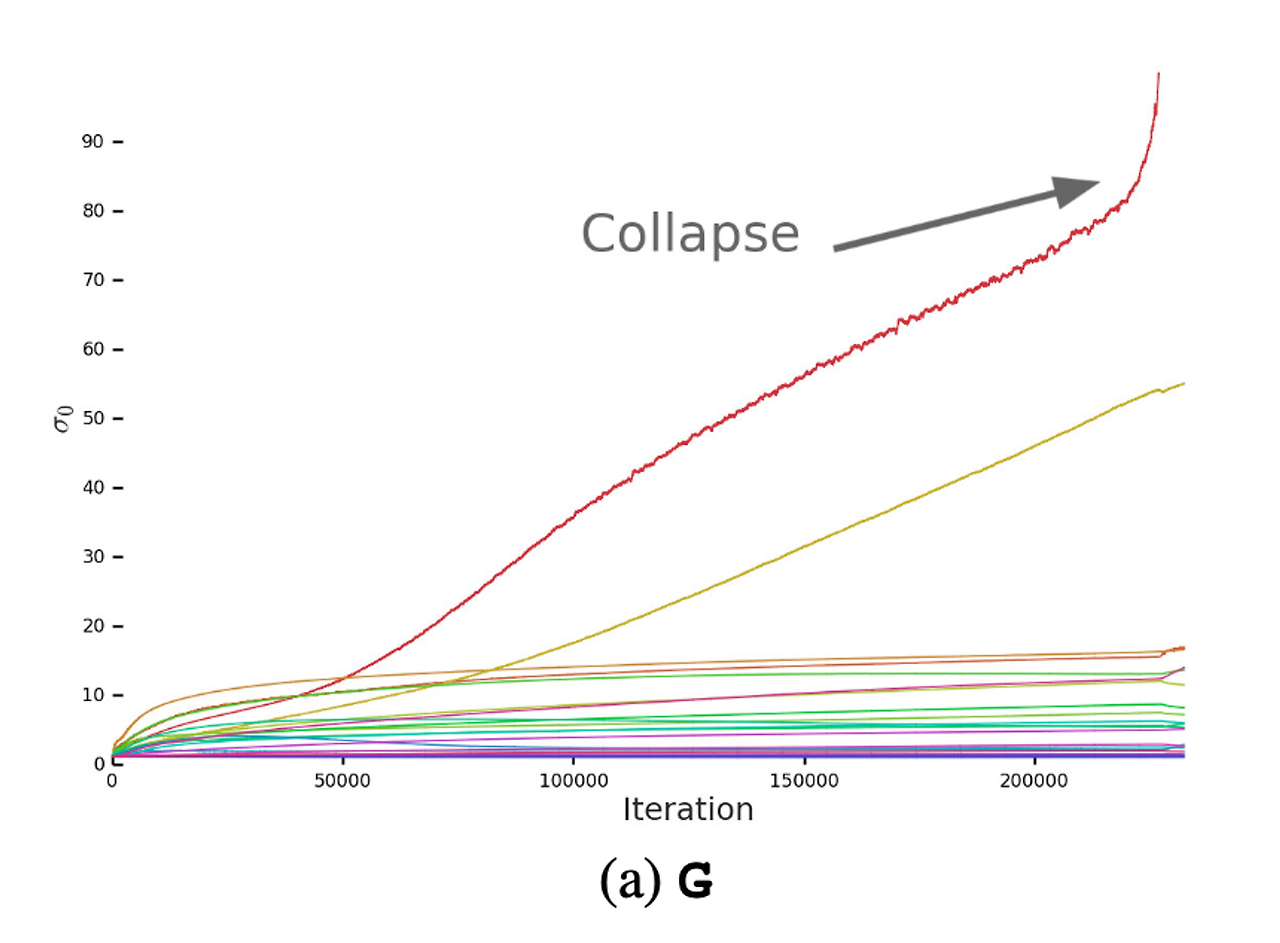
- 해당 그래프를 살펴보면, 대부분의 Generator 층은 well-behaved spectral norm인 것을 확인할 수 있지만, 몇 개의 층들은 ill-behaved된 것을 확인할 수 있음. 이러한 ill-behaved는 그래프에서 확인할 수 있듯이 spectral norm이 학습동안 커지다가 폭발하는 것을 확인할 수 있음
- 추가적인 조건을 Generator에 부과함으로써 이러한 spectral explosion을 카운터할 수 있는지 확인하였음.
- 먼저 각 가중치의 특이값들을 fixed value 이나 으로 regularize함. ( 2번째 특이값과 비율 r을 사용하여 나타내며, sg는 stop-gradient operation으로 특이값의 상승을 막기 위해 regularization을 해주는 것)
- 다른 대안으로, 부분적 partial singular value decomposition(SVD)을 사용하여 clamp 0을 나타내고, 주어진 가중치 행렬과 해당 행렬의 첫번째 특이값 벡터, 고정 첫번째 특이값 0을 clamp하기 위해 을 사용함. 실제 수식은 아래와 같음.
- clamp란, 사전적의미론 고정시키다는 뜻을, 함수로썬 주어진 범위를 벗어나지않도록 설정하는 것으로 해석 가능
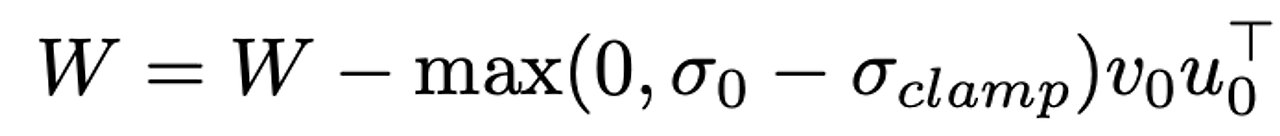
- 수식을 보면, 0이 (고정값)보다 커야 정상적으로 가중치 업데이트가 진행됨을 알 수 있으며, 는 나 로 설정함.
- Spectral Normalization의 유무에 상관없이 이러한 방법이 gradual increase와 explosion을 막는 효과를 내는 것을 확인하였음
- 하지만 이러한 경우에도, 약간의 성능만 향상시킬뿐, 결국 모델의 학습 붕괴를 완전히 막진 못했음
- 따라서 Generator의 개선만으로는 충분하지 않다 판단했고, Discriminator의 방법도 생각
Characterizing Instablility : The Discriminator
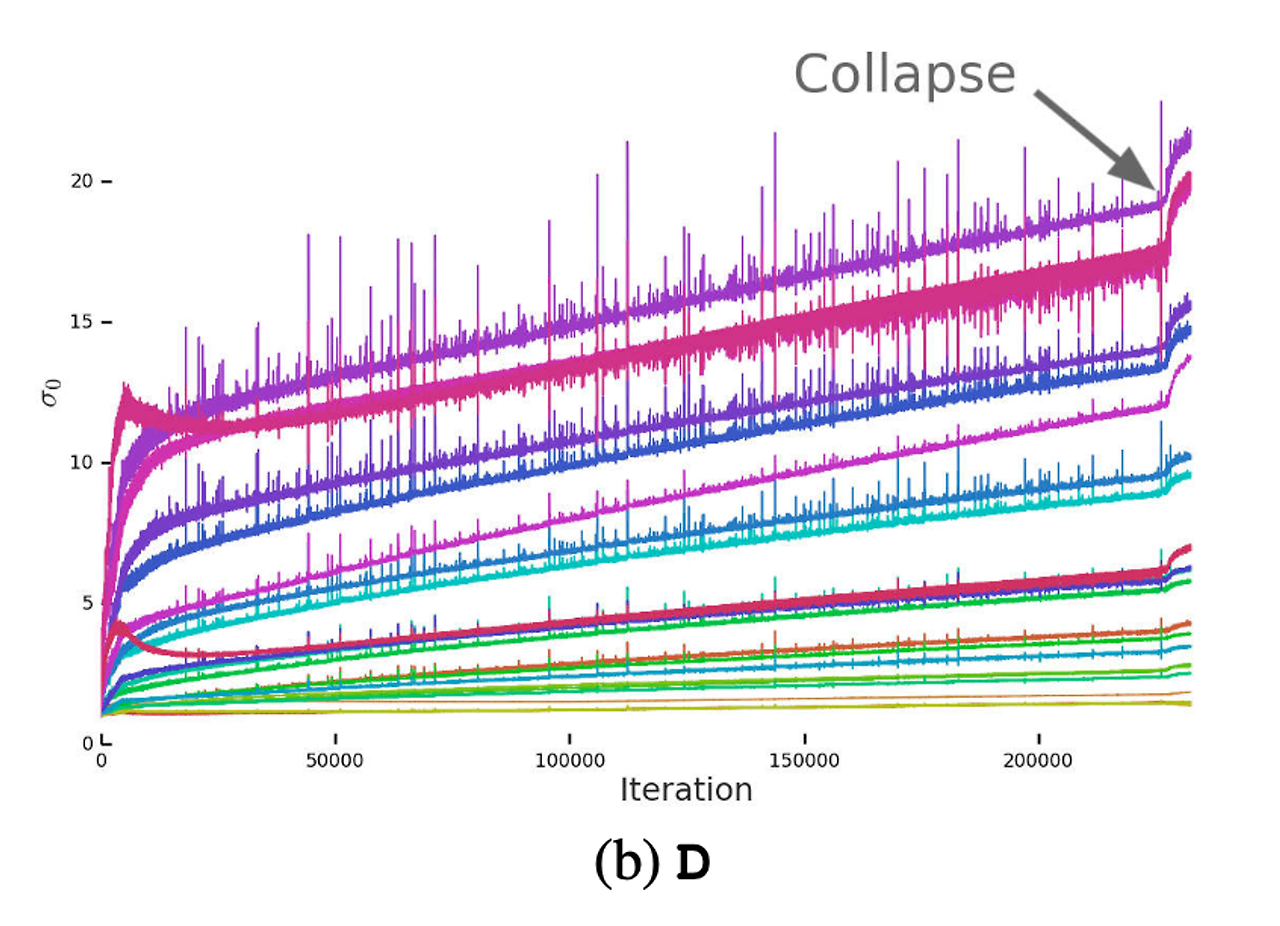
- 해당 사진은 Discriminator의 특이값 그래프이며, Noisy하고 특이값이 학습이 진행될 동안 Collapse에서 값이 확 뛰어오르는 것을 볼 수 있음
- 저자들은 이러한 노이즈가 적대적 학습의 최적화 과정으로 생기는 결과라고 가정하였으며, 이는 Generator가 배치를 주기적으로 생성하고, Discriminator가 해당 배치를 구별하느라 강하게 교란당하기 때문이라고 하였음
- 이러한 원인을 해결하기 위해서 gradient에 페널티를 주기로 하였고, Discriminator의 Jacobian 행렬에 규제를 주었음. 아래는 zero-centered gradient penalty.
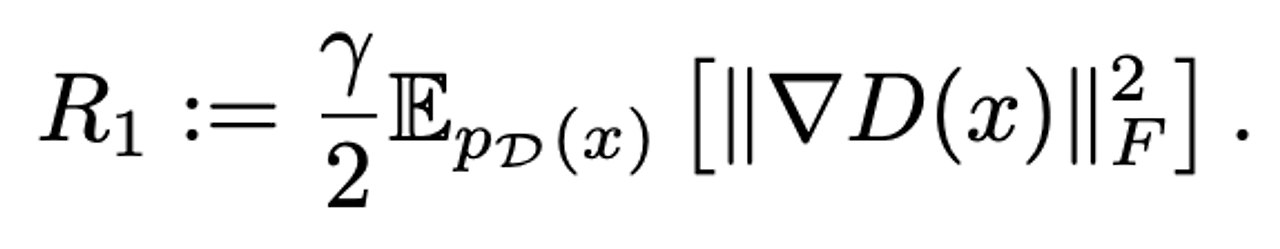
- 의 값을 10으로 하였을때 학습이 안정적이며, Generator와 Discriminator에서 smooth함과 boundednesss(제한)을 개선됨을 확인하였음. 그러나, 최종 퍼포먼스는 낮아졌는데(IS 45%감소), 이러한 증상을 완화시키기위해 부분적으로 이러한 페널티 감소를 줄였지만, 결과는 ill-behaved된 스펙트럼이 늘어났음
- 의 값을 1로 하였을때, (이 값이 붕괴가 일어나지않는 제일 최소임) IS의 감소가 약 20%로 개선됐음
- 이러한 실험을 다양한 셋팅(Orthogonal Regularization, Dropout, L2)으로 해보았고, 비슷한 증상을 나타냈음.
- 따라서 높은 페널티를 줄 수록, 학습의 안정성은 보장되지만, 퍼포먼스에 있어 상당한 손해가 발생함
- 또한, Discriminator의 Loss는 0에 가까워지지만 학습시간동안, 붕괴를 겪으면 높게 치솟게 되며, 이러한 증상의 이유는 Discriminator가 Overfitting 되었다. 라고 설명할 수 있었음. (Training example들 모두 외워버림)
- 간단한 테스트를 통해서 모델이 이렇게 example들을 모두 외워버리는지 확인하였고, 정말 Discriminator가 training set을 외우지만, 이것이 Discriminator의 역할이자, Generator에게 학습데이터와 유용한 학습 시그널을 제공함을 알 수 있었음
Experiments

- a)~ c)까지 BigGAN모델의 결과(threshold = 0.5) d)는 Class leakage 결과
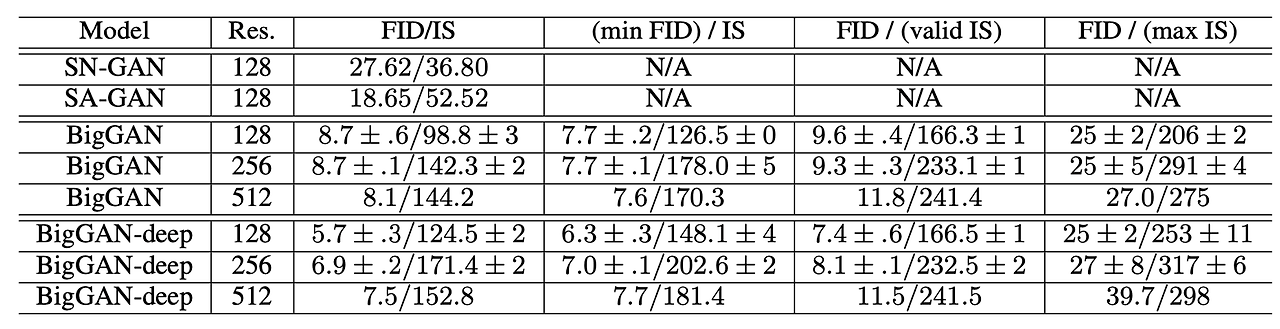
- 표는 각각 다른 해상도의 모델의 결과. 순서대로 Truncation이 적용되지 않은 일반 스코어, 가장 FID가 좋은 결과, IS의 validation결과, 가장 IS가 좋은 결과를 나타냄

- JFT-300M 데이터셋에서 진행한 BigGAN결과, Validation set은 IS 50.88, FID는 1.94의 값을 기록함
Conclusion
- 해당 모델은 ImageNet을 사용한 GAN모델의 새로운 레벨의 퍼포먼스를, 기존 SOTA보다 월등히 높은 결과를 얻었음
- 또한 학습 시 GAN의 반응을 분석하면서, 그들의 안정성을 가중치들의 특이값들로 characterize하였음.
- 마지막으로, 안정성과 퍼포먼스 사이 상호작용을 이야기하면서 마무리하였음
주석 1. Skip-Connection : 이전 layer의 정보를 직접적으로 Direct하게 이용하기 위해 이전 층의 정보를 연결하는 개념. ResNet에도 있음. 즉, 한마디로 입력 데이터가 네트워크의 여러 레이어를 건너뛰어 출력 레이어에 직접 연결되는 방식
주석 2. Moving Average : 이동평균. 평균을 구하되, 구하고자 하는 전체 데이터에 대한 평균이 아니라, 전체 데이터의 일부분 씩 순차적으로 평균을 구함
주석 3. Conditional Batch Normalization : Class-conditional 종류의 Batch normalization, Embedding으로 부터 를 예측함. 즉, GAN에서 class information이 Batch Normalization parameter에 영향을 주도록 하는데, 의 Embedding을 통해서 를 예측함
주석 4. Truncation : 범위에서 벗어난 것을 범위안에 들어오도록 Re-sampling하는 것. 해당 논문에 사용된 Truncated toward zero란, 특정값을 0에 가깝게 만들기 위해 그 값을 변경( 버림과 유사한듯) 2.7 → 2 , -2.7 → -2
주석 5. Orthogonal regularization : 직교성 (Orthogonality)는 직교행렬에 의한 곱셈이 기존 행렬의 norm이 변하지 않게함. (직교행렬 : , Norm은 벡터의 크기) 해당 Regularziation은, 깊은 모델의 터지거나 사라지는. 안좋은 상황에서 좋음. 가중치를 직교하게 유도하는 것이 핵심이며, → 얼마나 직교행렬에 가까운지 추정함!
주석 6. Singular Value : 특이값. Singular Value Decomposition : SVD. 즉 특이값 분해 → U, V = Orthogonal Matrix, Σ= Diagnol Matrix. 구하는 방법은 검색참고 ..
이상입니다.
이제 개강도 했겠다.. 일주일에 한편씩 논문을 꾸준히 리뷰할 수 있도록 노력해보려 합니다. 그다음엔 DCGAN, SNGAN 새로운 Multi-modal 논문 등이 업로드 예정입니다.