Multiple Linear Regression
Multiple features(Variables) = x1, x2, x3, x4 , ..

features of i th training example : i th Row vector
여러개의 x를 f_wb에 대입해주면 아래와 같다.

Vectorization(벡터화)
아래는 각 내적을 나타내는 방법이며, numpy의 dot함수를 나타냈을때 가장 simple한 것을 확인할 수 있음.

makes efficient ; scale to large datasheets
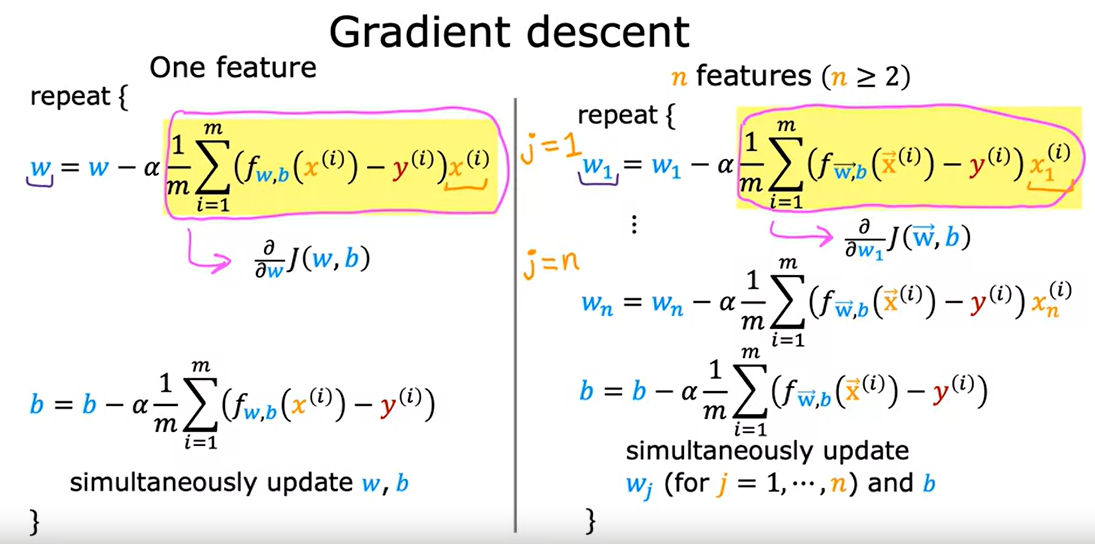
Gradient descent 에서의 Vectorization 활용

여러개의 feature로 바뀜에 따라 W_n을 각각 맞춰 해결해야함. 해당사항은 아래 참고
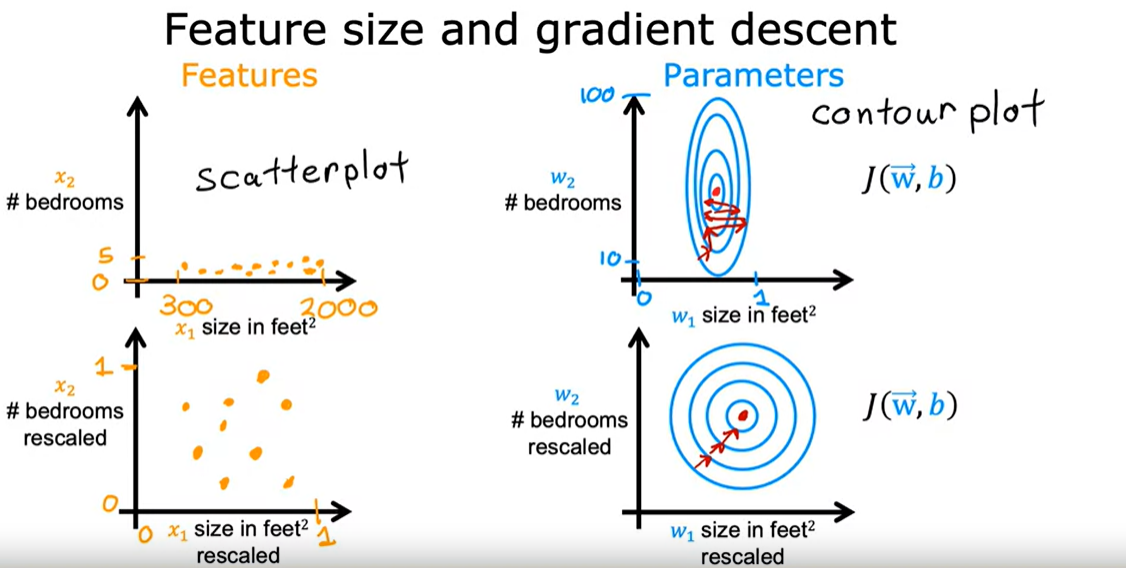
Feature Scaling(데이터 전처리 방법에 속하며 입력변수의 크기를 조정해주어 일정범위내로 바꾸는 방법)
Feature scale 의 예시
단위를 0< <1 로줄인다면 해당 J(w,b)의 변화를 직관적으로 확인가능
Mean Normalization(평균 정규화) : 값이 -1에서 1까지로 범위가 잡히는 것
헤당 방법은 Training set 의 X(i)의 평균을 mu(i) 라 하며, 아래의 예시와 같다.

Z-Score normalization (정규분포(혹은 가우시안 분포) 를 사용하여 정규화)
Standard deviation(표준편차)을 이용하여 마찬가지로 모든 training set의 x(i)와 평균 mu(i)의 차를 표준편차로 나눔.
예시참고

Feature scaling을 할 수 있는 방법은 위와 같은 방법들이 존재하며, 아래는 경우에 따라 필요한지를 따져 보는 예시이다.

Learning Curve
X축에는 Gradient descent를 시도한 횟수(iteration)을, y축에는 J(w,b)를 작성하므로써 횟수가 늘어남에 따라 J(w,b)가 어디로 수렴하느지 확인할 수 있음. 이에 따라 learning rate a가 올바르게 설정되었는지 아닌지 또한 확인할 수 있다.

만약 J(w,b)가 0.001보다 작다면 convergence로 선언가능.
learning rate가 너무 크다면 오류발생.
learning rate a를 매우 작게하여 계산을 하는것도 올바른 머신러닝이나 코드가 작성되었는지 확인할 수 있는 방법 중 하나
또한 매우작은 learning rate a부터 차근차근 구하여 최적의 learning rate를 구하는 방법 또한 존재
최종적으로 횟수에 비해 J(w,b)가 큰 learning rate인 경우 작은 learning rate를 시도,
반대로 횟수에 비해 미비한 변화의 J(w,b)라면 일정 배수의 learning rate를 사용하여 시도 하는 것이
올바른 Learning rate a를 찾는 방법

Polynomial Regression (다항 회귀)
Multiple linear Regression + Feature Engineering = Polynomial Regression
3가지의 경우가 있다.

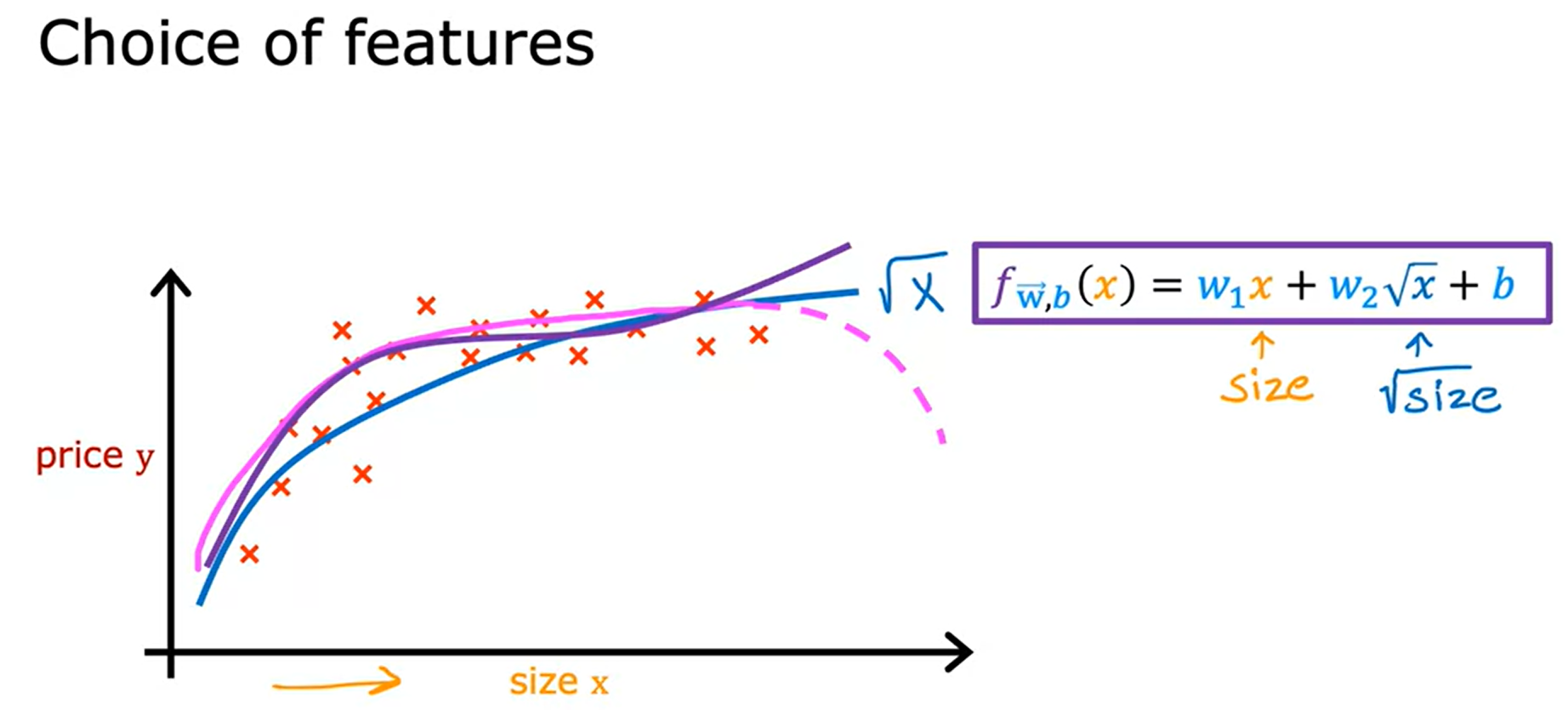
이차식이 들어가있는 경우, 해당 예시의 price y가 내려가는 그래프를 나타내는것을 예상할 수 있고,
따라서 우상향을 그리기 위해서는 삼차항 또한 더해주어 위와 같은 그래프를 나타낼 수 있다.
마지막으로 때론, 제곱근을 사용하기도 하는데, 이는 절대 아래로 내려가지않는 특성이 있으며,
다항식을 사용하여 그래프를 나타내거나 제곱근을 사용하여 나타내는 방법을 잘 선택하여 f(w,b)함수를 선택해야함.
'Deep Learning' 카테고리의 다른 글
| StarGAN-V2 구현하기 (0) | 2022.12.26 |
|---|---|
| HigherHRNet : Model 구현 (0) | 2022.11.20 |
| WSL 시간 동기화 하기 (0) | 2022.11.06 |
| Paper Review : HigherHRNet (0) | 2022.11.05 |
| What is Machine Learning (0) | 2022.07.15 |